Hydrostatik
Grundlagen der Hydrostatik
Die Hydrostatik beschäftigt sich mit den physikalischen Gesetzen in Flüssigkeiten. Ein wichtiges Gesetz hat jeder schon kennen gelernt, der im Wasser getaucht ist. Dabei spürst du Druck auf den Ohren – das hat etwas mit dem so genannten hydrostatischen Druck zu tun.
Grundsätzlich gilt: Der Wasserdruck nimmt mit der Tiefe zu – je tiefer du tauchst, desto größer wird das Druckgefühl auf den Ohren. Der Druck ist dabei von der Stellung der gedrückten Fläche unabhängig; der Druck ist also überall auf deinem Ohr gleich.
Als Faustregel gilt: Der Wasserdruck nimmt pro 10 Meter (m) Tiefe um ungefähr 1 bar zu. Achtung, den Luftdruck von 1 bar musst du mitberechnen, da dieser als normaler Luftdruck in Meeresspiegelhöhe auf dem Wasser aufliegt.
In einer Formel ausgedrückt sieht der hydrostatische Druck (p) so aus:
p = ρ • g • h
ρ = Dichte
g = Erdbeschleunigung
h = Höhe des Flüssigkeitsspiegels
Also:
Der hydrostatische Druck p ist (neben der Erdbeschleunigung, die ja immer gleich ist) nur von der Flüssigkeitstiefe h und der Dichte ρ der Flüssigkeit abhängig – und nicht von der Größe der Fläche.
Grundlagen der Hydrostatik
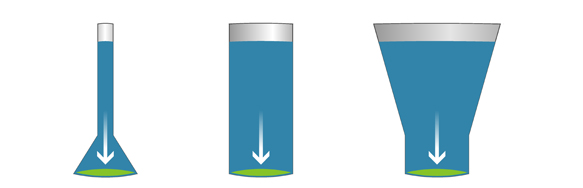
Das hat eine interessante Auswirkung. Vergleiche diese drei Gefäße miteinander!
In welchem Gefäß ist der Flüssigkeitsdruck des Wassers am Boden (grün markiert) am höchsten? Spontan würde man erwarten, dass der Druck im linken Gefäß geringer ist als im rechten, oder? Das stimmt aber nicht!
Die richtige Antwort scheint im ersten Moment verwirrend:
Der Druck ist überall identisch. Die Erklärung dafür ist einfach: Die Dichte der Flüssigkeit ist gleich, und die Flüssigkeitstiefe auch. Damit ist auch der hydrostatische Druck gleich.
Die Flüssigkeitsmenge in einem Gefäß ist hingegen nicht von Bedeutung. Dieses Phänomen bezeichnet man auch als hydrostatisches Paradoxon.